Fibroblast

Fibroblasts are the most common cells of connective tissue.

Fibroblasts and fibrocytes are two states of the same cells, the former being the activated state, the latter the less active state, concerned with maintenance. Currently, there is a tendency to call both forms fibroblasts.

Fibroblasts are morphologically heterogeneous with diverse appearances depending on their location and activity. 

Like other cells of connective tissue, fibroblasts are derived from primitive mesenchyme.

Fibroblasts have a branched cytoplasm surrounding an elliptical, speckled nucleus having one or two nucleoli. Active fibroblasts can be recognized by their abundant rough endoplasmic reticulum. Inactive fibroblasts, which are also called fibrocytes, are smaller and spindle shaped. They have a reduced rough endoplasmic reticulum. Although disjointed and scattered when they have to cover a large space, fibroblasts when crowded often locally align in parallel clusters.

The main function of fibroblasts is to maintain the structural integrity of connective tissues by continuously secreting precursors of the extracellular matrix. Fibroblasts secrete the precursors of all the components of the extracellular matrix, primarily the ground substance and a variety of fibres. The composition of the extracellular matrix determines the physical properties of connective tissues.

Physiology

Endocrine:

Hormone:
A hormone is a chemical substance that is secreted into the body fluids by one cell or a group of cells and has a physiological control effect on other cells of body.

Classification of Hormone:
I) according to the chemical nature:

1. Protein or peptides:

• ant. pituitary hormones
• post. pituiary hormones.
• pancreatic: insulin , glucagon
• parathyroid hormone

2. Steroids:
Adrenocortical hormone
Sex hormones
3. Derivatives of amino acid tyrosin:
Thyroid hormone
Adrenal medullary hormones (Epinephrine and norepinephrine)
II) according to the site of action:

1. General :
2.Local:
3.Tropoical:

Hormone Receptors

1. Cell membrane receptors: for protein and peptide hormones
2 Cytoplasmic receptors: for steroids

3. Nuclear receptors: for thyroid

FUNCTION OF ATP :

Virtually all forms of life use ATP, a nearly universal molecule of energy transfer. The energy released during catabolic reactions is stored in ATP molecules. In addition, the energy trapped in anabolic reactions (such as photosynthesis) is trapped in ATP molecules.

The function of ATP is to store energy within a cell. This way, energy within the body is not wasted, and can be stored for later use.( Biological Rechargable Battery)

ATP is referred to as currency because it can be “spent” in order to make chemical reactions occur. The more energy required for a chemical reaction, the more ATP molecules must be spent.

ATP serves as the major energy source within the cell to drive a number of biological processes such as  muscle contraction, and the synthesis of proteins. Extracellularly, ATP has been found to act as a neurotransmitter .

ATP receptors are widespread through the body. On its own it is known to have effects in the arteries, intestines, lungs, and bladder. It is also often released in tandem with other neurotransmitters, perhaps to add chemical stability.

Maintain energy dependant cell transport.

Pharmacokinetics Concept

The LADME scheme

LADME describes the pharmacokinetic processes which follow a given dosage regimen.
L = Liberation, the release of the drug from it's dosage form.
A = Absorption, the movement of drug from the site of administration to the blood circulation.
D = Distribution, the process by which drug diffuses or is transferred from intravascular space to extravascular space (body tissues).
M = Metabolism, the chemical conversion or transformation of drugs into compounds which are easier to eliminate.
E = Excretion, the elimination of unchanged drug or metabolite from the body via renal, biliary, or pulmonary processes.

Although LADME processes generally follow the above sequence, these are not discrete events. That is, one process is still occurring while the next one begins. Each event continues to occur well into the next. In fact, all five processes may occur simultaneously. Consider the case of a sustained release drug, the core of the SR tablet may still be liberating drug while previously absorbed drug is being eliminated.
LADME processes can be divided into two classes, drug input and drug output.

Input processes are:
L = Liberation, the release of the drug from it's dosage form.
A = Absorption, the movement of drug from the site of administration to the blood circulation.

The term commonly used to describe the rate and extent of drug input is bioavailability. Drugs administered by intravenous routes exhibit essentially 100% bioavailability.

Output processes, or disposition of drug are:
D = Distribution, the process by which drug diffuses or is transferred from intravascular space to extravascular space (body tissues).
M = Metabolism, the chemical conversion or transformation of drugs into compounds which are easier to eliminate.
E = Excretion, the elimination of unchanged drug or metabolite from the body via renal, biliary, or pulmonary processes.

Because our main focus is on IV administered drugs, the remainder of this review will concentrate on output processes.
---------------------------------------------------------------------------------------------------
Distribution

Distribution is the process by which a drug diffuses or is transferred from intravascular space to extravascular space (body tissues). These spaces are described mathematically as volume(s) of distribution.

In the simplest of terms, a drug's volume of distribution is that volume of bodily fluid into which a drug dose is dissolved. Therefore, if we know the dose that was given, and we can measure the serum level (concentration), then we can calculate a volume:
Volume of distribution = Dose / drug concentration

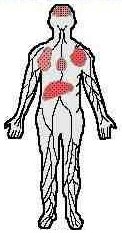
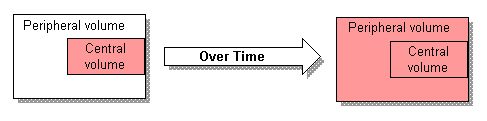
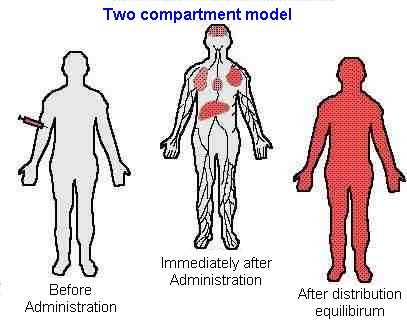
Of course, the human body is not a glass beaker. Drug is distributing in and out of many tissue compartments while it is simultaneously being eliminated. This complex and continually changing environment must be simplified in order to mathematically model the human body. Therefore, the body is usually divided into two spaces, a central and a tissue compartment.

Central volume (Vc)
The central volume of distribution (Vc) is a hypothetical volume into which a drug initially distributes upon administration. This compartment can be thought of as the blood in vessels and tissues which are highly perfused by blood.

Central volume of distribution (Vc) may be calculated as:
Vc = Dose / Peak serum level
Note: by rearranging this equation we can see that dose and Vc are the primary determinates of the peak level:
Peak = Dose / Vc

Peripheral volume (Vt)
The peripheral volume is the sum of all tissue spaces outside the central compartment. Of course, all peripheral tissues are not homogenous, this is a simplification for the purpose of creating a usable mathematical model.

All drugs initially distribute into the smaller Vc before distributing into the peripheral volume. Together, Vc and Vt create the apparent volume of distribution (Vd).


------------------------------------------------------------------------------------------------
Apparent volume of distribution (Vd)
Apparent Vd is a term used to describe the volume of fluid that would be required to account for all drug in the body. It does not necessarily refer to any identifiable compartment in the body. It is simply the size of a compartment necessary to account for the amount of drug in the body. Because Vd is hypothetical in nature, it is referred to as an apparent volume.

As you will see, distribution volumes are important for estimating:
Amount of drug in the body
Peak serum levels
Clearance

Summary
To review, the most commonly used volumes of distribution are:
Central volume (Vc)
Tissue (or peripheral) volume (Vt)
Apparent volume of distribution (Vd)
------------------------------------------------------------------------------------------------
Elimination

Drugs are cleared primarily by the liver and kidneys. Excretion into the urine is a major route of elimination for metabolites and unchanged drug.

Most drugs are eliminated by a first-order process. With first-order elimination, the amount of drug eliminated is directly proportional to the serum drug concentration (SDC).

With first order elimination, at a certain point in therapy, the amount of drug administered during a dosing interval exactly replaces the amount of drug excreted. When this equilibrium occurs (rate in = rate out), steady-state is reached.
---------------------------------------------------------------------------------------------
Clearance (CL)
Clearance is a descriptive term used to evaluate efficiency of drug removal from the body. Clearance is not an indicator of how much drug is being removed; it only represents the theoretical volume of blood which is totally cleared of drug per unit time. Because clearance is a first-order process, the amount of drug removed depends on the concentration.

Clearance can be thought of as the proportionality constant that makes the average steady-state drug level equal to the rate of drug administration. Clearance (rate out) can be calculated from the dose (rate in) and average steady-state concentration:
Cl = (Dose / interval) / Cpss ave

Elimination rate constant (Kel)
With first-order elimination, the rate of elimination is directly proportional to the serum drug concentration (SDC). There is a linear relationship between rate of elimination and SDC. Although the amount of drug eliminated in a first-order process changes with concentration, the fraction of a drug eliminated remains constant. The elimination rate constant (Kel) represents the fraction of drug eliminated per unit of time.

Here is an example of a first order process:
Time
(hrs) Amount remaining
in body Amount
eliminated Fraction
eliminated
0 1000 - -
1 850 150 0.15
2 723 127 0.15
3 614 109 0.15
4 522 92 0.15
5 444 78 0.15


The serum level curve observed from a drug eliminated by a first order process:














A plot of this same data using a log scale on the y-axis results in a straight line

The slope of this straight line correlates to Kel.

Mathematically, this relationship may be represented by the following equation. If we plug in post-distribution serum levels (i.e., peak and trough levels), and the time difference between them, we can calculate a Kel which is specific for this patient:
Kel = ln(Peak / Trough) / time

Once we have the Kel, we can rearrange this equation to predict the time it takes to reach a specific serum level. If we plug our target peak and trough levels in, then we can use this equation to calculate an ideal dosing interval (tau):
tau = ln(Peak / Trough) / Kel
---------------------------------------------------------------------------------------------

Half-life (t ½)
Another important parameter that relates to the rate of drug elimination is half-life (t ½). The half-life is the time necessary for the concentration of drug in the plasma to decrease by half. Both t ½ and Kel attempt to express the same idea, how quickly a drug is removed, and therefore, how often a dose has to be administered. An important relationship between t ½ and Kel can be shown by mathematical manipulation:
T ½ = 0.693 / Kel

Relationship between Kel, Vd, and CL
Kel (and t ½) are dependent upon clearance and the volume of distribution. However, it is invalid to make any assumptions about the Vd or CL of a drug based solely upon knowledge of its half-life.
Kel = CL / Vd

Summary
Most drugs are eliminated by a first-order process.
Steady-state is that equilibrium point where the amount of drug administered exactly replaces the amount of drug excreted.
Clearance represents the theoretical volume of blood which is totally cleared of drug per unit time.
Kel represents the fraction of drug eliminated per unit of time.
The slope of a log-scale serum level decay curve correlates to Kel.
t ½ is the time necessary for the concentration of drug in the plasma to decrease by half.
-------------------------------------------------------------------------------------------------
Pharmacokinetic modeling

Pharmacokinetic models are relatively simple mathematical schemes that represent complex physiologic spaces or processes. Accurate PK modeling is important for precise determination of elimination rate.

The most commonly used pharmacokinetic models are:
1-compartment
2-compartment

One compartment model
All drugs initially distribute into a central compartment (Vc) before distributing into the peripheral compartment (Vt). If a drug rapidly equilibrates with the tissue compartment, then, for practical purposes, we can use the much simpler one-compartment model which uses only one volume term, the apparent volume of distribution, Vd.

Example
The distribution phase for aminoglycosides is only 15-30 minutes, therefore, we can use a one-compartment model with a high degree of accuracy.

Serum level plot for a 1-compartment model
Yields a straight line when using a log scale on the y-axis.



Two compartment model
Drugs which exhibit a slow equilibration with peripheral tissues, are best described with a two compartment model.

Example
Vancomycin is the classic example, it's distribution phase is 1 to 2 hours. Therefore, the serum level time curve of vancomycin may be more accurately represented by a 2-compartment model.

Serum level plot for a 2-compartment model
Yields a biphasic line when using a log scale on the y-axis.

Distribution phase
During the initial, rapidly declining distribution phase, drug is moving from the central compartment to the tissue compartment.

Elimination phase
Elimination of drug is the predominant process during the second phase of the biphasic plot. Because elimination is a first-order process, the log plot of this phase is a straight line.

Note: You should also note from this graph that failure to consider the distribution phase can lead to significant errors in estimates of elimination rate and in prediction of the appropriate dosage. This is especially important with vancomycin. Unless you are using a two-compartment model, you should not use a level drawn during the distribution phase to calculate the elimination rate.
Summary
A one-compartment model may be used for drugs which rapidly equilibrate with the tissue compartment, e.g, aminoglycosides.
A two-compartment model should be used for drugs which slowly equilibrate with the tissue compartment, e.g, vancomycin.
A log scale plot of the serum level decay curve of a 1-compartment model yields a straight line.
A log scale plot of the serum level decay curve of a 2-compartment model yields a biphasic line.
Failure to consider the distribution phase can lead to significant errors in estimates of elimination rate.
-----------------------------------------------------------------------------------
Therapeutic drug monitoring

The basic goal of therapeutic drug monitoring (TDM) is to enhance the patient's chance of maximum benefit from a prescribed drug while minimizing the risks of toxicity. Characteristics of drugs associated with TDM are:
Narrow therapeutic range.
Unpredictable dose/response relationship.
Significant consequences from toxicity.
Correlation between SDCs and efficacy or toxicity.
Readily available assays.
-------------------------------------------------------------------------------------------
Steady state
As successive doses are administered, drug begins to accumulate in the body. With first order elimination, at a certain point in therapy, the amount of drug administered during a dosing interval exactly replaces the amount of drug excreted (rate in = rate out). When this equilibrium occurs, the peak and trough drug concentrations are the same for each additional dose given. When peak and trough concentrations are the same with two or more successive doses, steady-state is reached.
The time required to reach steady-state is approximately 4 to 5 half-lives.
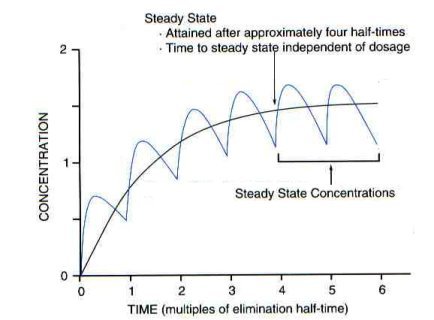
Note:You should note from this graph that failure to evaluate steady-state levels can lead to significant errors in estimates of elimination rate and in prediction of the appropriate dosage. Therefore, serum sampling is best performed at steady-state.

Timing serum level draws
Serum samples must be drawn during the elimination phase, when net distribution is complete.
Note: You should note from this graph that failure to consider the distribution phase can lead to significant errors in estimates of elimination rate. An accurate measure of Kel can only be obtained when serum levels are drawn in the elimination phase.

Dhaka Medical MD: Microbiology

Dhaka Medical MD: Microbiology

PHARMA NOTES

Pharmacokinetics:

Definition:

quantitative study of absorption, distribution, metabolism, and elimination of chemicals in the body, as well as the time course of these effects.

Pharmacokinetics is the study of what the body does to a drug.

Pharmacodynamics is the study of what a drug does to the body.

Summary:
- absorption
- distribution
- metabolism
- elimination
Administration=When the drug is given

Absorption=When the drug is taken up by the body

Distribution=When the drug spreads through the body

Elimination=When the drug is removed from the body

Pharmacokinetics Principle:

Pharmacon=Medicine

Kinesis=Movement.

• Concentration of a drug at its site of action is a fundamental determinant of its pharmacologic effects.

• Drugs are transported to and from their sites of action in the blood – because of that: the concentration at the active site is a function of the concentration in the blood.

• The change in drug concentration over time in the blood, at the site of action, and in other tissues is a result of complex interactions of multiple biologic factors with the physicochemical characteristics of the drug.

Pharmacokinetic Concepts: Rate Constants and Half-Lives

• Disposition of most drugs follows first-order kinetics – a constant fraction of the drug is removed during a finite period of time.
• The absolute amount of drug removed is proportional to the concentration of the drug
• In first-order kinetics, the rate of change of the concentration at any given time is proportional to the concentration present at that time.
• When the concentration is high, it will fall faster than when it is low.

• First-order kinetics apply not only to elimination, but also to absorption and distribution.

Half-Lives

• The rapidity of pharmacokinetic processes is often described with half-lives

• Half-Life = the time required for the concentration to change by a factor of 2.
• 
  Half-Life = the period of time required for the concentration or amount of drug in the body to be reduced to exactly one-half of a given concentration or amount.

• Half-Life = the time required for half the quantity of a drug or other substance deposited in a living organism to be metabolized or eliminated by normal biological processes. Also called biological half-life.

Drug Elimination:

• Elimination = all the various processes that terminate the presence of a drug in the body.

• Processes:
  - metabolism
  - renal excretion
  - hepato-biliary excretion
  - pulmonary excretion (inhaled anesthetics mainly)
  - other: saliva, sweat, breast milk, tears

Renal Excretion:

• Both metabolically changed and unchanged drugs
• LMW substances: filtered from blood through the Bowman membrane of the capsule
• Some: actively secreted
• Reabsorption in the tubule: depending on the lipid solubility, degree of ionization, molecular shape, carrier mechanism (for some).
• Weak acid: best reabsorbed from an acidic urine.
  Important to know if the drug is dependent on renal function or excretion.

Hepatobiliary Excretion:

• Drugs metabolites – excreted in the intestinal tract with the bile.
• Majority: reabsorbed into the blood and excreted through urine. (enterohepatic cycle).
• Poorly lipid-soluble organic compounds – at least three active transport mechanisms

Pulmonary Excretion:

• Volatile anesthetics and anesthetic gases: in large part eliminated unchanged through the lung
• The factors that determine uptake operate in reverse manner

DRUG ABSORPTION AFTER ORAL ADMINISTRATION:

First Order Kinetics:

A constant fraction of the drug in the body is eliminated per unit time. The rate of elimination is proportional to the amount of drug in the body. The majority of drugs are eliminated in this way.

The Volume of Distribution (Vd) is the amount of drug in the body divided by the concentration in the blood. Drugs that are highly lipid soluble, such as digoxin, have a very high volume of distribution (500 litres). Drugs which are lipid insoluble, such as neuromuscular blockers, remain in the blood, and have a low Vd.

The Clearance (Cl) of a drug is the volume of plasma from which the drug is completely removed per unit time. The amount eliminated is proportional to the concentration of the drug in the blood.

The fraction of the drug in the body eliminated per unit time is determined by the elimination constant (kel). This is represented by the slope of the line of the log plasma concentration versus time.

Cl = kel x Vd

Rate of elimination = clearance x concentration in the blood.

Elimination half life (t1/2): the time taken for plasma concentration to reduce by 50%. After 4 half lives, elimination is 94% complete.

It can be shown that the kel = the log of 2 divided by the t1/2 = 0.693/t1/2.

Likewise, Cl = kel x Vd, so, Cl = 0.693Vd/t1/2.

And t1/2 = 0.693 x Vd / cl

The rate of elimination is the clearance times the concentration in the plasma

Roe = Cl x Cp

Fraction of the total drug removed per unit time = Cl/Vd.

If the volume of distribution is increased, then the kel will decrease, the t1/2 will increase, but the clearance won't change.

Confused?

Example: You have a 10ml container of orange squash. You put this into a litre (ok 990ml!) of water. The Vd of the orange squash is 1000ml. If, each minute, you empty 10ml of the orange liquid into the 10ml container, discard this, and replace it with 10ml of water. The clearance is 10 ml per minute. The elimination half life is: 70 minutes . The kel is Cl/Vd = 10/1000 = 0.01. Shown the other way, 0.693/50 = 0.01.

If the volume of the container is increased to 2000ml, then the clearance remains the same, but the Vd, and consequently the t1/2, increases (to 140 minutes).

Simple, isn't it?

What is described above is a single compartment model, what would occur if the bloodstream was the only compartment in the body (or if the Vd = the blood volume). But the human body is more complex than this: there are many compartments: muscle, fat, brain tissue etc. In order to describe this, we use multicompartment models.

Multicompartment Models:

Why does a patient wake up after 5 minutes after an injection of thiopentone when we know that it takes several hours to eliminate this drug from the body? What happens is that, initially the drug is all in the blood and this blood goes to "vessel rich" organs; principally the brain. After a few minutes the drug starts to venture off into other tissues (fat, muscle etc) it redistributes, the concentration in the brain decreases and the patient wakes up! The drug thus redistributes into other compartments.

If you were to represent this phenomenon graphically, you would follow a picture of rapid fall in blood concentration, a plateau, and then a slower gradual fall. The first part is the rapid redistribution phase, the alpha phase, the plateau is the equilibrium phase (where blood concentration = tissue concentration), and the slower phase, the beta phase, is the elimination phase where blood and tissue concentrations fall in tandem. This is a simple two compartment model and is as much as you need to know.

An couple of interesting pieces of information can be derived from the log concentration versus time graph. If you extrapolate back the elimination line to the y axis, then you get to a point called the CP0 - a theoretical point representing the concentration that would have existed at the start if the dose had been instantly distributed (dose/Vd). From this new straight line you can figure out how long it takes for the concentration to drop by 50%: the elimination half life. Likewise, a similar procedure can be performed on the α phase: the redistribution half life.

While it is very important that you understand these concepts, the reality is that most drugs are infinitely more complicated that this, and computer calculations are required to derive this data.

Bioavailability:

This is the fraction of the administered dose that reaches the systemic circulation. Bioavailability is 100% for intravenous injection. It varies for other routes depending on incomplete absorption, first pass hepatic metabolism etc. Thus one plots plasma concentration against time, and the bioavailability is the area under the curve.

Zero Order Elimination:

Why if I have 10 pints (PINT= Unit of volume in the U.K) of beer before midnight will I fail a breathalyser (Braeth Analyser) test at 8 am the following morning? Either this is due to alcohol having a very long half life (which it does not) or that alcohol is cleared in a different way.

What happens is that the metabolic pathways responsible for alcohol metabolism are rapidly saturated and that clearance is determined by how fast these pathways can work. The metabolic pathways work to their limit. This is known as zero order kinetics: a constant amount of drug is eliminated per unit time. This form of kinetics occours with several important drugs at high dosage concentrations: phenytoin, salicylates, theophylline, and thiopentone (at very large doses). Because high dose thio is very slow to clear, we no longer use it in infusion for status epilepticus (as it takes ages for the patient to wake up!).

=================================================================

Cardiac Uses of β-blockers (CARDIOSELECTIVE ):
1. Mild to Moderate Hypertension
2. Angina Pectoris.
3. Arrhythmias
4. prophylaxis of MI (Post MI)
5. hypertrophic obstructive cardiomyopathy (Heart disease characterised by thickening of the internal heart muscle and a blockage inside the heart)

Non-Cardiac Uses:

1. Thyrotoxicosis
2. Migraine
3. Glucoma
4. Essential tremon
5. Anxiety.
6. Pre-surgical management of adrenal gland tumours (phaeochromocytoma), but only in combination with an alpha blocking medicine

Role of Propranolol in thyrotoxicosis:

The clinical manifestations of hyperthyroidism have suggested to physicians for many years that the sympathetic nervous system may be involved in their production. Despite this, the precise interrelationship between the thyroid gland and the sympathetic nervous system has never been defined but controlled investigations have shown that hypersensitivity to catcholamines does not occur in animals or man with artificially produced thyrotoxicosis.

In recent years beta-adrenoceptor blocking drugs, and in particular propranolol, have been used in patients with hyperthyroidism. Evidence exists that they control some of the peripheral manifestations of the disease, including nervousness, palpitations, tachycardia, increased cardiac output and tremor, but they do not appear to affect the underlying thyrotoxic process itself.

Propranolol has been used with sucess in the treatment of
1. acute hyperthyroid crisis Or Thyroid Storm:

40 mg orally 6 hourly or,

1mg slowly I.V (not exceeding 1mg/min.)
It rapidly decreases heart rate, usually within 2 to 3 h when given orally and within minutes when given IV.

2. In tachycardia or atrial fibrillation with thyrotoxicosis, particularly in elderly, because antithyroid drugs usually take several weeks to become fully effective.

3. in pre-operative preparations for thyroidectomy,

4. for the control of symptoms and signs following the administration of radioactive iodine therapy and antithyroid drugs,

5. during the period of diagnostic thyroid investigations and

6. occasionally as the sole therapy.

• 
  
  
  
  
  
  
  
  

Celllular Organelle

Organelle are specialized subunit within a cell that have specific functions.

Types:

          MEMBRANOUS: 

• Mitochondria
• Endoplasmic Reticulum
• Golgi Complex

• Lysosome
• Peroxisome

           NON-MEMBRANOUS:

• Ribosome
• Centrosome
• Microtubules
• Microfilaments

Cytoskeleton

Cytoskeleton:
  Can be defined as highly organized network of structural proteins responsible for maintaining the shape and organization of cells and promoting movement.
 
The cytoskeleton comprises 3 proteins:
1. Microtubules
2. microfilament
3. intermediate filaments.
Microtubules:
  Unique to eukaryotes. Microtubules are small intracellular tubes composed subunit proteins termed tubulin. (i.e. Polymer of tubulins)
Tubulins are of 2 types : α and β.
One alpha- and one beta-tubulin form a heterodimer.
Under appropriate conditions tubulin subunits polymerize to form microtubules.
Polymerization is guided by a variety of structures:
• basal bodies.
• centrioles
• centromeres os chromosome.

Collectively these 3 structures is known as Microtubules Organizing Centres (MTOCs)

                                                                       

                                             

   



Functions:
   

ANATOMY

Epithelium : is comprised of cells which cover

•  the exterior surfaces of the body (skin, front of eye)
•  line  the internal closed cavities of the body (thoracic [lungs], pericardial [heart] and abdominal [guts]) and
• those body tubes which communicate with the exterior (the alimentary [GI tract], respiratory [lungs] and genitourinary tracts [kidneys, bladder etc]).

Epithelium also forms the secretory portion of glands and their ducts, and the receptors of certain sensory organs (e.g. taste buds; olfactory [smell]cells).

The cells forming the epithelium are in close contact with one another.

They may be arranged in

• multiple layers, as in the covering of the exterior surfaces of the body where protection and impermeability are primary requirements, or
• in a single layer, as in the lining of most of the internal surfaces of the body. 

POLARISATION:

All epithelia exhibit a free surface at their apex, and on the opposite surface, they adhere to a basement membrane. Thus they are polarized cells. This polarity is maintained by the various intercellular junctions, which bind the cells together and by molecules which bind the epithelial cells to the basement membrane. Thus the apical side of an epithelial cell is generally quite different (structurally and biochemically) from the basal side. 

Blood vessels do not normally penetrate the epithelium,Nutrition of the epithelium thus depends on the diffusion of metabolites through the basal lamina.

Since epithelia cover free surfaces of the body, they are often subject to abrasion, thus they are constantly replaced. As cells at the free surface are sloughed off or die, cells sitting on the basement membrane (basal cells) divide and differentiate into the various cells which comprise the epithelium.

Classification of Epithelia.

Classification of the various epithelia of the body is based solely on the arrangement and shape of the cells. The terminology used is thus unrelated to function and serves only for descriptive purposes.  
Simple: one cell thick: 

stratified, two or more cells thick.  

Epithelia (both simple and stratified) are further described according to the shape of the cells forming the surface layer.

The individual cells comprising the surface layer of the epithelium may be described as:

squamous, where the width and depth of the cell is greater than its height (like a fried egg);

cuboidal, where the width, depth and height are approximately the same (like a cube):

columnar, where the height of the cell appreciably exceeds the width or depth.  

To complicate this simple classification, two special categories of epithelium are typically included, namely pseudostratified and transitional epithelium.

 

 

Microbiology

Differences btn Eukaryote and Prokaryote :

Need to Know Bcoz:
It is the basis of antibiotic therapy
To understand Selective toxicity

Main differences:
Neuclear Membrane
Cell Wall (specific for prokaryotes ; pro=before, karyote= nucleus
Ribosomal Structure (prokaryote = 70s, Sub-units 50s &30s)

#Each ribosome is made up of two small sub-units ; as for eukaryote 80s(60s &40s)
s= Svendberg (pronounciation vad- berg;
The unit is named after the Swedish chemist Theodor Svedberg (1884-1971), winner of the Nobel prize in chemistry in 1926 for his work in the chemistry of colloids and his invention of the ultracentrifuge.)

's' is determind by the rate of sedimantation in a centrifuge machine.

=============================================================

Plasmodium:

Life Cycle of Plasmodium
The sexual cycle occurs in the mosquito and the sporozoites in mosquito saliva
are injected into the host while feeding on human blood. Asexual reproduction
happens in the human host, and it consists of the exoerythrocitic cycle followed by
the erythrocytic cycle.

1) Exoeryrocytic cycle
 Injected sporozoites travel to liver (takes 1 hour), penetrate and
infect liver parenchymal cells 
 Sporozoites divide inside cell over a period of 1.5 weeks
(asymptomatic). 
 Infected cell ruptures and releases merozoites into blood
circulation

2) Erythrocytic cycle
 Merozoites infect RBCs.
 Merozites form into “signet ring” - trophozoite
 RBC develops into a schizont, which ruptures releasing merozoites
 The merozoites infect other RBC’s (amplification)
 Some merozoites will develop into the sexual haploid form:
macrogametocyte (female) or a microgametocyte (male). The
mosquito picks this up and the sexual cycle occurs
 Bursting RBC = symptoms (1.5 – 2 weeks of replication inside
RBC’s)

o Fever every 3-4 days, paroxysms of shaking chills
o Symptoms when other organs involved
o Hemolysis: icterus, jaundice, enlarged spleen
o Make sure to ask about travel!
 Non-immunologic mechanisms for controlling malaria:
o Spleen – traps RBC
 Outcome: death or chronic illness

3) Sexual Cycle in mosquito: the definitive host

 Gametocytes picked up in blood meal
 Male gametocyte pairs up with female and develop into oocyst in gut
 Thousands of sporozoites develop inside oocyst, escape from oocyst,
and move to salivary gland ready to be injected into humans.
 Mosquito cycle (sexual) gives the malaria diversity so that there is
drug resistance. The gametocytes are taken up and in the stomach the
sporozoites are released and go to the saliva. (slide 40) It would be
great to prevent oocysts formation in the stomach or sporozoitic life in
the saliva. There are many targets (e.g. exflagellation of
microgametocyte).
P. Falciparum

Pathogenesis

 Destruction of erythrocytes
 Liberation of parasite and erythrocyte material into the circulation.
 Host rxn to these events – TNF alpha and other inflammatory mediators; Release
of cytokines after glycolipid release on merozoite rupture
 A moving junction moves the parasite into the RBC. Once inside of the RBC
attachment factors are expressed on RBC – histadine-rich proteins that cause
attachment of RBC’s to the capillaries and postcapillary venules leading to
sequestration. In the early stages of P. falciparum you may not find RBC that are
infected because they are all lodged in the postcapillary venules. Ultimately once
there are enough parasites in the circulation you will pick them up when a thin
prep blood smear is performed.
 It is thought that this type of instability in blood flow leads to poor oxygenation
that leads to cerebral malaria, which is the primary cause of death. Cytokine
release has an impact on this process. P. falciparum’s unique sequestration in
micro-circulation of vital organs interfering with flow and metabolism
preferentially involves the white brain matter, heart, kidney, liver (hence cerebral
malaria). 
 The classic fever pattern for P. falciparum is every 3 days once it synchronizes.
This tertian pattern of fevers was recorded as long ago as Hippocrates time.

=============================================================

• The characteristic fever spike has been correlated with incremental rises in serum levels of TNF-a associated with the release of parasite proteins during erythrocytic rupture.
• IMMUNE RESPONSE 
  
  The immune response to malaria is not well understood. The presence of serum antibodies in individuals living in regions where malaria is endemic indicates that the immune system mounts a humoral response against the parasite. This immunity is strain-specific and can be lost if the individual migrates to a region where malaria is not endemic. Furthermore, the efficacy of the humoral response is limited by the intracellular tendencies of the parasite as well as its ability to alter its surface molecules through various maturational stages. The humoral response is bolstered by a variety of non-specific effector mechanisms. The presence of excess type-1 cytokines, including IFN-g , IL-2, IL-12, and TNF-a , has been confirmed in infected individuals. However, the ability of the infected to generate CTL activity is severely limited; the infected hepatocytes are the only cellular targets expressing the requisite class I MHC molecule.
  
  
  

Biochemistry

ELECTROLYTES PROFILES:

4 Major electrlytes (Na+,K+,HCO3-,Cl- ) and determination of body fluid conc. of those electrolytes are grouped
under a familial test of Elec. profiles.

Functions of Elec. :-
1. Body water homeostasis
2. Acid-Base balance
3. Regulation of muscle function (cardiac,smooth,skeletal)
4. Ruling electron transfer reaction
5.Co-factor for enzymes.


Fractional Excretion of Electrolytes:

(MEANING TUBULAR EXCRETION IS <1%)
An electrolyte conc. in urine is a useul indicator of renal handling of water and elec.

While GFR is considered as the best overall indicator of renal function, fractional excretion (FE) tests have been also proposed, especially for assessment of tubular function.
In renal physiology, FE of electrolytes is defined as the fraction of filtered electrolytes which escapes reabsorption and consequently is excreted in urine.
FE of an electrilyte (X) is calculatd using a random urine sample with simultaneously obtained serum sample for x and Cr.
So, FE x = (Urine X/Plasma X) * (Pls. Cr./Urn. Cr.) * 100 [xpressed as %]

Clinically Na+ is the most measured to distinguished renal from non-renal (pre-renal) causes of decreasedNa. So, for Na…

FE Na (%) =(Urn. Na. / Plasma Na.) * (Pls. Cr. /urn. Cr.) *100
Interpretation FE Na. :
No reference interval has been established
Elevation of FE for Na has been suggested as a means to differentiate azotemia due to intrinsic renal disease from that due to prerenal factors.
Another indication of FE test is Fanconi’s syndrome. Abnormal FE values however may be found in normal renal function (eg in primary hyperparathyroidism). A large number of factors (e.g. creatinine assay, age, diet, drugs) may moreover induce misinterpretation of FE.

In most normal subjects, the fractional excretion of sodium is usually less than 1 percent but may be raised with an increase in salt intake.
In acutely azotemic patients, a low fractional excretion of sodium ( <1%) usually indicates a prerenal process that is responsive to volume repletion. That is avid Na. Retention to compensate for xtr-renal fluid losses (vomiting, diarhoea, sewting or 3rd space losslike ascites).
A fractional excretion >1% in acutely azotemic patients usually indicates intrinsic renal injury,
(but is consistent with volume depletion in patients receiving diuretics,mineralocorticoid defeciency or in some patients with salt-losting nephropathy or chronic renal insufficiency)

Osmolarity /Osmolality:

Osmole: particle present in a soln. E.g. Na in plasma.
Osmolality: Osmoles per Kg of water.
Osmolarity: Osmoles per Liter of soln.
I n body fluids 2 measurement are so closed that they can used interchangeably.


Normal Osmolality:
280—295 mmol/L
Calculation =
2*Na. (mmol/L) +Glucose (mmol/L) + Urea (mmol/L).
So, if glucose and urea are normal then only 2*Na. Will do.

Osmoler Gap:
Disparity btn measuered osmolality (in Lab by an OSMOMTER) and the calculated osmolality.

Osm. Gap. =
Measured osmolality – Calculated osmolality.

Why not calculated minus measured?
Other osmotical substances increases the measured without altering Serum Na and therefore ,
Measured >Calculated osmolality.

PART - I course

Paper I :
Anatomy :
Histology, Basic Genetics, Embryology,Neuroanatomy.
Pharmacology.

Paper II :
Physiology :Gen Physio, Resp. CNS, CVS, Endo, Renal
(Tutorial : Blood, Sp. Senses)
Biochemistry:


Paper III : Pathology & Microbiology.